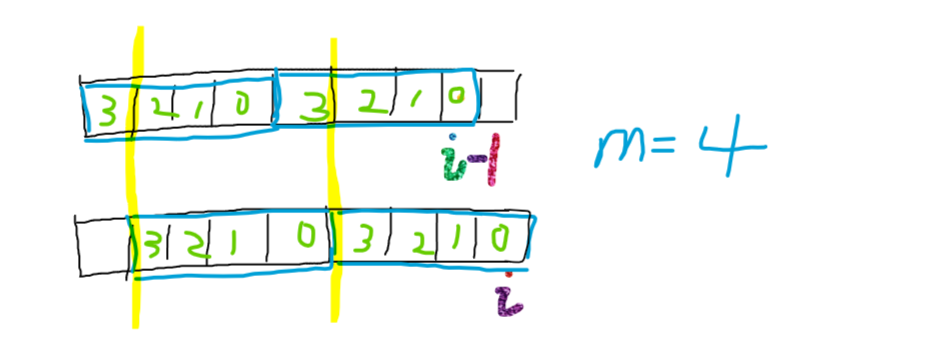ECF-69-2

Educational Codeforces Round 69 (Rated for Div. 2)

A.DIY Wooden Ladder

找最长的的俩个，然后看是能放的木板多，还是给的木板多

B.Pillars

观察发现这个序列有三种情况满足题意

1.一直上升

2.一直下降

3.先上升后下降

C.Array Splitting

我们可以得到一个差分数组，观察发现，如果我们只要一个序列，就是把差分数组全部加起来，要俩个子序列就是从差分数组的某个位置切一刀，并且切的后面的数去掉，这样我们就发现，其实就是要去除m-1个差分数组中的数，当然选前n-1大喽

reverse//反转元素顺序

差分数组真正用法传送门

代码：

/*-------------------------------------------------------------------------------------------*/
int a[MAX];
/* ------------------------------------------------------------------------------------------*/
 
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    //freopen("input.in","r",stdin);
    //freopen("output.out","w",stdout);
/* --------------------------------------------------------------------------------------*/
    cin >> N >> M;
    int sum = 0;
    multiset<int,greater<int>> a;
    int x,y;
    cin >> x;
    int n;
    for(int i = 1;i < N;i++)
    {
        cin >> y;
        n = y - x;
        sum += n;
        a.insert(n);
        x = y;
    }
    int cnt = 0;
    int add = 0;
    for(auto it = a.begin();;it++)
    {
        if(cnt == M-1) break;
        add += *it;
        cnt++;
    }
    cout << sum -add <<endl;
    return 0;
}

D.Yet Another Subarray Problem

哇，这个题肝了一下午，终于看懂了别人的题解，官方题解不知道他在说些什么，这个题解的dp设置的好巧妙啊，佩服了

参考题解传送门

题目思路：

dp[i][j] 表示以第i个数为右端点，长度 %m == j的区间的最大值

左端点在哪里我们并不关心，我们保证长度 % m == j的区间最大

初始化的话，因为存在一些不可取的值，而且题目的可能ans是负数，所以dp要设置为-INF

状态转移方程：

第一种：

就是当余数是1的时候，根据题目的式子向上取整，多出来的这一位就要多去减一次K

特殊情况就是M == 1的时候，每加一个数就要去减一次K，需要特判，不然就会一直走第二种情况（仔细思考）

第二种：

当j == 0是，恰好是一个整区间，应该从余数为M - 1递推

第三种:

其他情况

为什么递推可以从dp[i-1][j-1] + a[i];得到呢？

来看这个图，假如m = 4；绿色为余数，蓝色为一个大小为m的区间，黄色线是要取到的范围的左边界

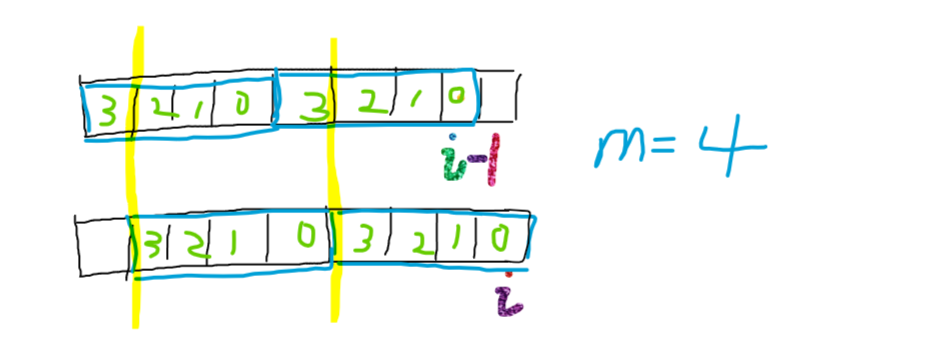
假如我们现在取余数j = 3的时候，是不是发现i-1时余数j == 2覆盖的区间正好和下面差一个a[i]

if(j == 1 || M == 1)
{
    dp[i][j] = max(dp[i-1][0] + a[i] - K,a[i] - K);
}
else if(j == 0)
{
    dp[i][j] = dp[i-1][M-1] + a[i];
}
else
{
    dp[i][j] = dp[i-1][j-1] + a[i];
}

题目代码：（思路一下午，代码五分钟）

LL T,N,M,K;
/*-------------------------------------------------------------------------------------------*/
LL a[MAX];
LL dp[MAX][MAX_1];
/* ------------------------------------------------------------------------------------------*/

int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    //freopen("input.in","r",stdin);
    //freopen("output.out","w",stdout);
/* --------------------------------------------------------------------------------------*/
    cin >> N >> M >> K;
    for(int i = 1;i <= N;i++)
    {
        cin >> a[i];
    }
    for(int i = 0;i < MAX;i++)
    {
        for(int j = 0;j < MAX_1;j++)
        {
            dp[i][j] = -INF;
        }
    }
    LL ans = 0;
    for(int i = 1;i <= N;i++)
    {
        for(int j = 0;j < M;j++)
        {
            if(j == 1 || M == 1)
            {
                dp[i][j] = max(dp[i-1][0] + a[i] - K,a[i] - K);
            }
            else if(j == 0)
            {
                dp[i][j] = dp[i-1][M-1] + a[i];
            }
            else
            {
                dp[i][j] = dp[i-1][j-1] + a[i];
            }
            ans = max(ans,dp[i][j]);
        }
    }
    cout << ans <<endl;
    return 0;
}