15ICPC沈阳

B - Bazinga

题目思路：

1.ac自动机多个串匹配咱也不会

2.kmp一个个搜会tle -> 500 * 500 * 4000​

3.参考博客

进一步分析我们可以发现，对于第ｊ串字符串，倘若前ｊ串都是ｊ的字串，那么我们下一步只需要判断ｊ是否是ｊ＋１的字串即可（因为如果ｊ是ｊ＋１的字串，而前ｊ串又是ｊ的字串，易得ｊ＋１串也是前ｊ串的字串，进而得出前ｊ＋１串是ｊ＋１串的字串。）

而倘若ｊ串并不是ｊ＋１串的字串，那么下一步只需判断ｊ串是否是ｊ＋２串的字串即可。

my：

如果j不是i的子串，那么答案直接就可以是max（ans，j）

如果j是i的子串，那么1-j的所有串也是i的子串，所以j++，继续比，保证j < i

通过维护j的位置，来保证同一个子串集合内的父子串一定会被匹配到

（看到一篇博客说，如果j不是i的子串，那么j-1也不是i的子串，这话应该是错的，虽然跟这个思路没关系）

//f代表不是子串，->代表是子串
1 f 2
1 f 3
1 f 4
1 -> 5
2 -> 5
3 -> 5
4 f 5
(1,2,3)可以用5表示
4 -> 6
5 f 6
(1,2,3,4)可以用6表示
所以不会缺

KMP

啥是kmp呢？

复杂度为O(m + n)

参考博客

代码：

int KmpSearch(char* s, char* p)
{
	int i = 0;
	int j = 0;
	int sLen = strlen(s);
	int pLen = strlen(p);
	while (i < sLen && j < pLen)
	{
		//①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++    
		if (j == -1 || s[i] == p[j])
		{
			i++;
			j++;
		}
		else
		{
			//②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]    
			//next[j]即为j所对应的next值      
			j = next[j];
		}
	}
	if (j == pLen)
		return i - j;
	else
		return -1;
}

解释：

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

• 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
• 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。
• next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

next：

next的原理：

什么是前缀后缀：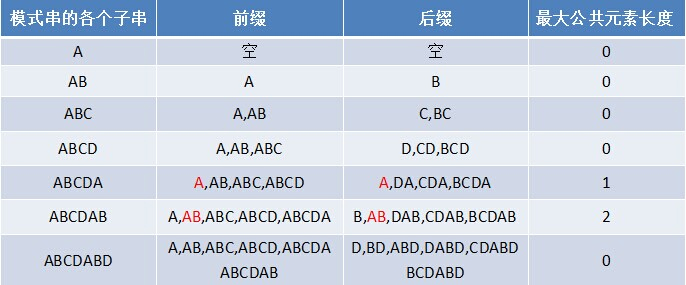

1. 寻找前缀后缀最长公共元素长度

   比如对于字符串aba来说，它有长度为1的相同前缀后缀a；而对于字符串abab来说，它有长度为2的相同前缀后缀ab（相同前缀后缀的长度为k + 1，k + 1 = 2）。

2. 求next数组

   next 数组考虑的是除当前字符外的最长相同前缀后缀，所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后，只要稍作变形即可：将第①步骤中求得的值整体右移一位，然后初值赋为-1

   比如对于aba来说，第3个字符a之前的字符串ab中有长度为0的相同前缀后缀，所以第3个字符a对应的next值为0；而对于abab来说，第4个字符b之前的字符串aba中有长度为1的相同前缀后缀a，所以第4个字符b对应的next值为1（相同前缀后缀的长度为k，k = 1）。

如何求next：

next[j] = k 代表p[j] 之前的模式串子串中，有长度为k 的相同前缀和后缀。有了这个next 数组，在KMP匹配中，当模式串中j 处的字符失配时，下一步用next[j]处的字符继续跟文本串匹配，相当于模式串向右移动j - next[j] 位。

下面的问题是：已知next [0, …, j]，如何求出next [j + 1]呢？

对于P的前j+1个序列字符：

• 若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1；
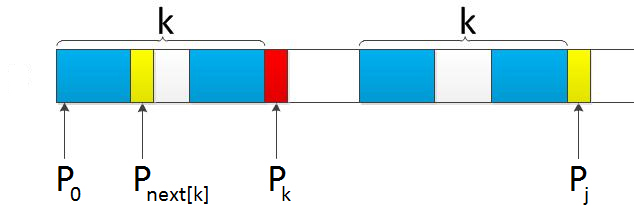
• 若p[k ] ≠ p[j]，如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] = next[k] + 1，否则继续递归前缀索引k = next[k]而后重复此过程。

（这个就无法言语表达，根据这个图来体会就比较好了）

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
a	b	c	d	a	b	f	n	m	a	b	c	d	a	b	p
-1	0	0	0	0	1	2	0	0	0	1	2	3	4	5	0

代码：

void GetNext(char* p,int next[])
{
	int pLen = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
		//p[k]表示前缀，p[j]表示后缀
		if (k == -1 || p[j] == p[k]) 
		{
			++k;
			++j;
			next[j] = k;
		}
		else 
		{
			k = next[k];
		}
	}
}

优化next：

问题出在不该出现p[j] = p[ next[j] ]。为什么呢？理由是：当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配），所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢？如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]。

代码：

//优化过后的next 数组求法
void GetNextval(char* p, int next[])
{
	int pLen = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
		//p[k]表示前缀，p[j]表示后缀  
		if (k == -1 || p[j] == p[k])
		{
			++j;
			++k;
			//较之前next数组求法，改动在下面4行
			if (p[j] != p[k])
				next[j] = k;   //之前只有这一行
			else
			//因为不能出现p[j] = p[next[j]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
				next[j] = next[k];
		}
		else
		{
			k = next[k];
		}
	}
}

题目代码：

/*-------------------------------------------------------------------------------------------*/
int mynext[MAX][MAX_1];
char str[MAX][MAX_1];
/* ------------------------------------------------------------------------------------------*/


void GetNextval(int n)//优化版的next
{
	int sLen = strlen(str[n]);
	mynext[n][0] = -1;
	int k = -1;
	int j = 0;
	while (j < sLen - 1)
	{
		if (k == -1 || str[n][j] == str[n][k])
		{
			++j;
			++k;
			if (str[n][j] != str[n][k])
				mynext[n][j] = k;
			else
				mynext[n][j] = mynext[n][k];
		}
		else
		{
			k = mynext[n][k];
		}
	}
}


bool KmpSearch(int s,int p)//kmp
{
	int i = 0;
	int j = 0;
	int sLen = strlen(str[s]);
	int pLen = strlen(str[p]);
	while (i < sLen && j < pLen)
	{
		if (j == -1 || str[s][i] == str[p][j])
		{
			i++;
			j++;
		}
		else
		{
			j = mynext[p][j];
		}
	}
	if (j == pLen)
		return true;
	else
		return false;
}


int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    //freopen("input.in","r",stdin);
    //freopen("output.out","w",stdout);
/* --------------------------------------------------------------------------------------*/
    cin >> T;
    for(int t = 1;t <= T;t++)
    {
        cin >> N;
        for(int i = 1;i <= N;i++)
        {
            cin >> str[i];
        }
        cout << "Case #" << t << ": ";
        int ans = -1;
        for(int i = 1;i < N;i++)
        {
            GetNextval(i);
        }
        int j = 1;
        for(int i = 2;i <= N;i++)//根据题目思路
        {
            while(i > j && KmpSearch(i,j))
            {
                j++;
            }
            if(i > j) ans = max(i,ans);
        }
        cout << ans <<endl;
    }
    return 0;
}

Pagodas-D

题目思路

可以发现，只要是M，N gcd 的数就可以达到

所以算出gcd 算出范围内可取的数的个数

分奇偶讨论