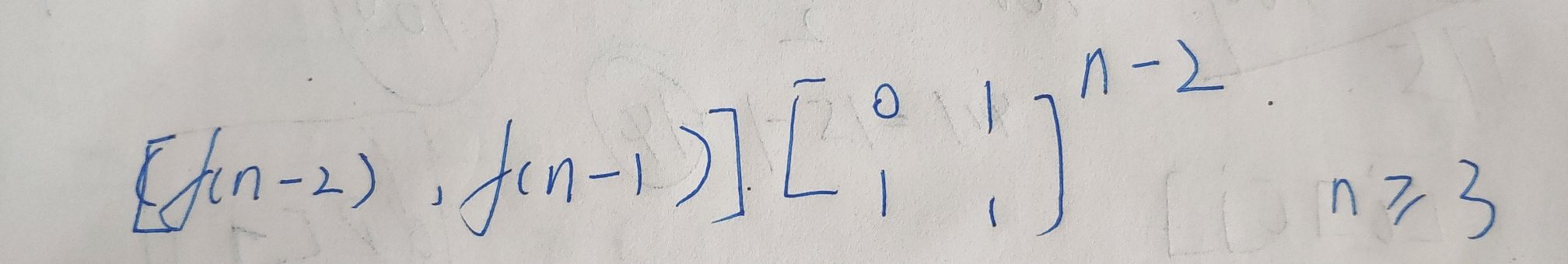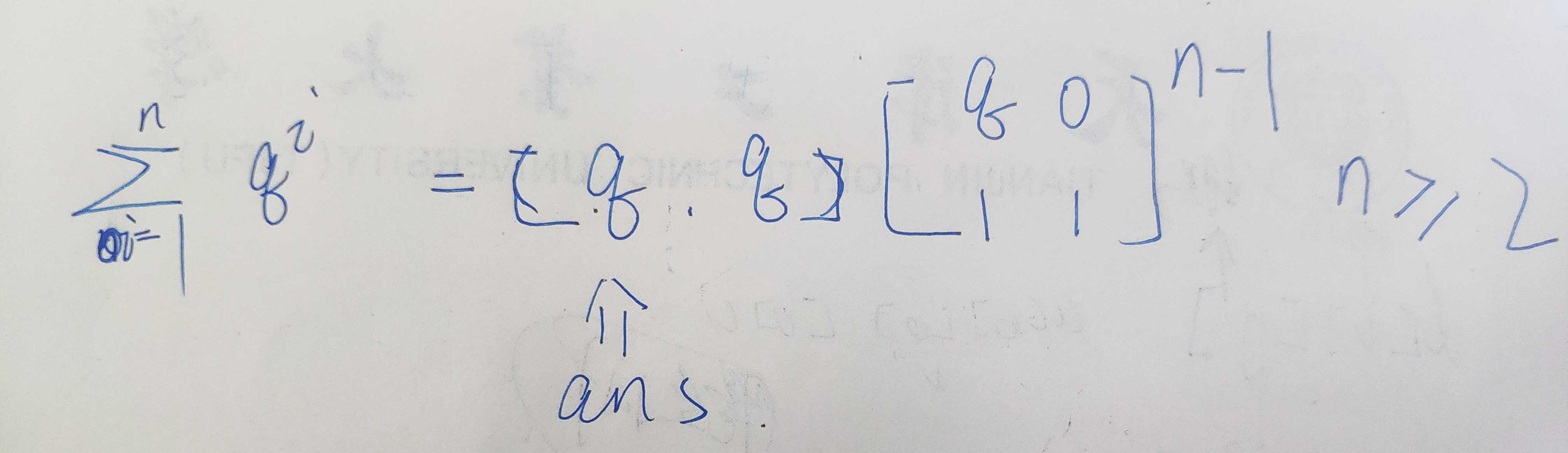普通的快速幂
1
2
3
4
5
6
7
8
9
10
11
12
13
| LL MODe(LL a,LL b)
{
LL sum = 1;
a %= MOD;
while(b)
{
if(b & 1)
sum = (sum * a) % MOD;
a = (a * a) % MOD;
b >>= 1;
}
return sum;
}
|
矩阵快速幂
就是把数字a,b变成矩阵来求
实例:POJ3070
https://vjudge.net/problem/POJ-3070
$f(i) = f(i-1) + f(i-2)$
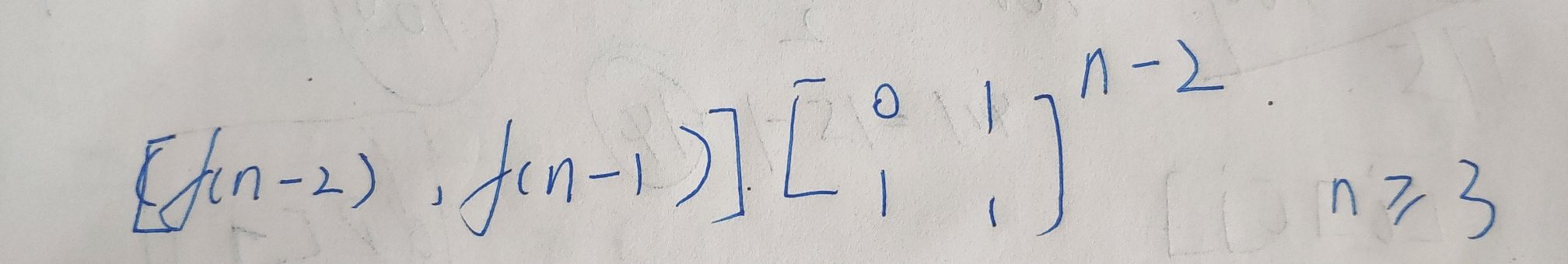
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
int a[MAX][MAX];
int b[MAX][MAX];
void calculate(int a[][MAX],int b[][MAX])
{
int c[MAX][MAX];
for(int i = 0;i < MAX_1;i++)
{
fill(c[i],c[i]+MAX,0);
}
for(int i =0;i < MAX_1;i++)
{
for(int j = 0;j < MAX_1;j++)
{
for(int k = 0;k < MAX_1;k++)
{
c[i][j] += (a[i][k]*b[k][j]) % MOD;
}
}
}
for(int i = 0;i < MAX_1;i++)
{
for(int j = 0;j < MAX_1;j++)
{
a[i][j] = c[i][j];
}
}
}
void Fibonacci(int n)
{
while(n)
{
if(n&1)
{
calculate(b,a);
}
calculate(a,a);
n >>= 1;
}
}
int main()
{
while(cin >> N && N != -1)
{
a[0][0] = 0;
a[0][1] = 1;
a[1][0] = 1;
a[1][1] = 1;
b[0][0] = 1;
b[0][1] = 0;
b[1][0] = 0;
b[1][1] = 1;
if(N == 0)
{
cout << 0 <<endl;
continue;
}
if(N == 1 || N == 2)
{
cout << 1 << endl;
continue;
}
Fibonacci(N-2);
cout << (b[0][1]+b[1][1]) % MOD << endl;
}
return 0;
}
|
实例2:
HBCPC-B
https://ac.nowcoder.com/acm/problem/25999
$$
s[i] = s[i - 1]*q + q
$$
把这个递推式变成矩阵乘法
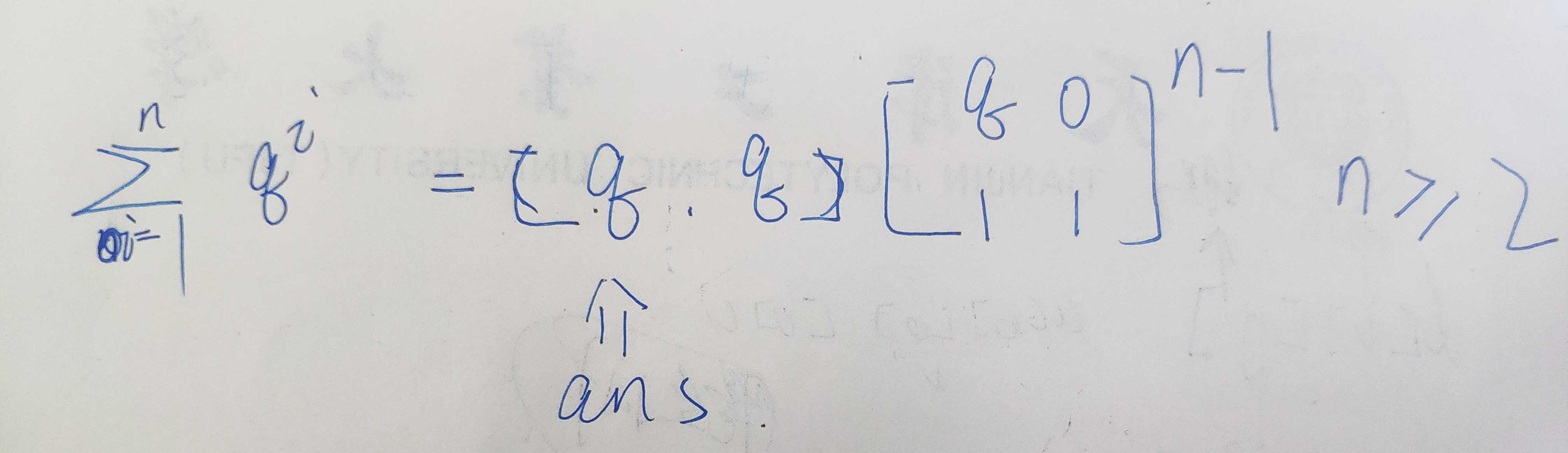
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
LL a[MAX][MAX];
LL b[MAX][MAX];
int main()
{
cin >> T;
while(T--)
{
LL n,q,mod;
cin >> q >> n >> mod;
q %= mod;
a[0][0] = q;
a[0][1] = 0;
a[1][0] = 1;
a[1][1] = 1;
b[0][0] = 1;
b[0][1] = 0;
b[1][0] = 0;
b[1][1] = 1;
if(n == 0)
{
cout << 1 <<endl;
continue;
}
if(n == 1 )
{
cout << q << endl;
continue;
}
dengbi(n-1,mod);
cout << ((b[0][0]+b[1][0]) *q) % mod << endl;
}
return 0;
}
|